いちょう祭オンライン企画
量子プログラミングをしてみよう
この記事のねらい
このページは 2025 年度のいちょう祭のために特設したオンライン企画ページです。高校 2 年生程度の物理や数学を理解しており、Python の基本文法を知っている読者を想定し、量子プログラミングに触れてみることを目標にします。
量子コンピュータに期待されること
量子コンピュータは、量子力学の原理を利用して計算を行う新しい計算機です。従来のコンピュータとは本質的に異なる性質を持つため、以下のような分野での革新が期待されています。
-
暗号解析:現在インターネットの通信や電子署名などに広く使われているRSA暗号という方式がありますが、これは現在の古典コンピュータでは解読が極めて困難です。ところが、量子コンピュータはShorのアルゴリズムによってこのRSA暗号を効率的に解読できる可能性があることが知られており、それだけでも非常に大きなインパクトがあると考えられています。
-
物質科学・創薬:原子や分子といったミクロなスケールの物理現象は量子力学に従っており、重ね合わせや量子もつれなどの性質を含むため、古典コンピュータによるシミュレーションは非常に困難です。一方で量子コンピュータは、自身が重ね合わせ状態を持つことで、こうした量子系のシミュレーションを効率的に行えることが理論的に示されています。これにより、ミクロな世界の理解が進むだけでなく、それが現実世界の物質の性質の理解にもつながり、将来的には新しい薬の設計や新材料の発見、さらには物理の基本原理の解明といった応用にもつながる可能性があるとして注目を集めています。
-
最適化・機械学習:この分野ではまだ探索段階ではありますが、量子コンピュータの能力を活かした新しいアルゴリズムの研究が進められています。例えば、QAOA(量子近似最適化アルゴリズム)を用いた組合せ最適化や、量子コンピュータでなければ実現できないようなタスクも徐々に見えてきています。こうした研究により、特定の問題においては量子コンピュータが古典的な手法よりも優れた性能を発揮する可能性が模索されています。
これらの理由により、量子計算は将来にわたって大きな社会的インパクトを持つ技術として期待されています。

古典ビットと量子ビット
量子コンピュータは、古典的なコンピュータとは異なり、「量子ビット(qubit)」と呼ばれる情報の単位を使って計算を行います。これは、従来のコンピュータが扱う「古典ビット」とは本質的に異なる性質を持っており、量子コンピュータの動作原理を理解する上で非常に重要なポイントとなります。
古典ビット
古典ビットは 0 または 1 のどちらか一方だけをとる情報の単位です。実際のコンピュータでは、トランジスタやキャパシタなどの電子素子によって実現されており、電圧の高低によって 0 と 1 が表現されます。もちろん物理的には中間の電圧値が存在することもありますが、論理回路の抽象化の中ではビットは常に 0 か 1 のどちらかに定まっているものとして扱われます。また、乱数を用いるようなアルゴリズムでは結果が一見ランダムに見えることもありますが、これは本質的には「どのように値が選ばれたのかを私たちが知らない」という無知に由来する不確実性です。つまり、古典ビットの不確実性は主観的な情報の欠如にすぎず、物理的な根拠をもって複数の状態が同時に存在するわけではありません。
量子ビット
量子ビットは、古典ビットとは異なり、0 と 1 の両方の状態が重ね合わさった状態(重ね合わせ状態)を取ることができます。量子力学においては「測定」という操作を行うまで、量子ビットは 0 と 1 のどちらかに決まっているわけではなく、両方が潜在的に同時に存在しているとされます。この「測定」とは、量子ビットの状態を観測して最終的に 0 または 1 のどちらかの値に収束させる操作のことであり、その結果は確率的に得られます。
ここで重要なのは、この不確実性は単なる無知ではなく、量子力学の法則そのものに基づく本質的な性質であるという点です。量子ビットの状態は、多世界解釈の立場から見ると「0 の世界」と「1 の世界」が同時に存在しているようなものと考えることもできます。そして、これらの世界線は独立しているのではなく、干渉を起こすことが可能です。この干渉により、ある操作を行うと 0 の確率を強めたり、逆に 1 の確率を打ち消したりすることができるのです。これは古典ビットでは絶対に起こらない現象であり、量子計算が持つ根本的な強みの一つとされています。場合によっては「負の確率」のような概念(厳密には確率ではないが、振幅の符号が影響する)を用いて記述されることもあり、古典的な直感では捉えきれない振る舞いが現れることもあります。
量子ゲートと量子計算
私たちがふだん使っているスマートフォンやパソコンのような古典的なコンピューターは、「論理ゲート(ロジックゲート)」と呼ばれる基本的な部品を組み合わせることで、さまざまな計算を実現しています。たとえば、「ANDゲート」は2つの入力が両方とも1のときだけ出力が1になるような回路であり、「NOTゲート」は0を1に、1を0にひっくり返すような回路です。これらの論理ゲートをたくさんつなげることで、計算機は四則演算や文字の表示など、あらゆる処理を行っています。
量子コンピューターでも、基本的な考え方は似ています。1つ1つの量子ビットに対して「量子ゲート」と呼ばれる操作を行い、それを組み合わせることで計算を進めていきます。量子ゲートは、量子ビットの状態を変えるための操作であり、古典的な論理ゲートに相当するものです。よく使われる量子ゲートには、状態をひっくり返す「Xゲート」、2つの量子ビットの間に関係をつくる「CNOTゲート」、状態を少しずつ回転させる「Ryゲート」、そして波のような性質に影響を与える「位相ゲート」などがあります。これらのゲートをうまく組み合わせることで、量子コンピューターは通常のコンピューターでは難しい複雑な問題の解決に挑戦することができるのです。
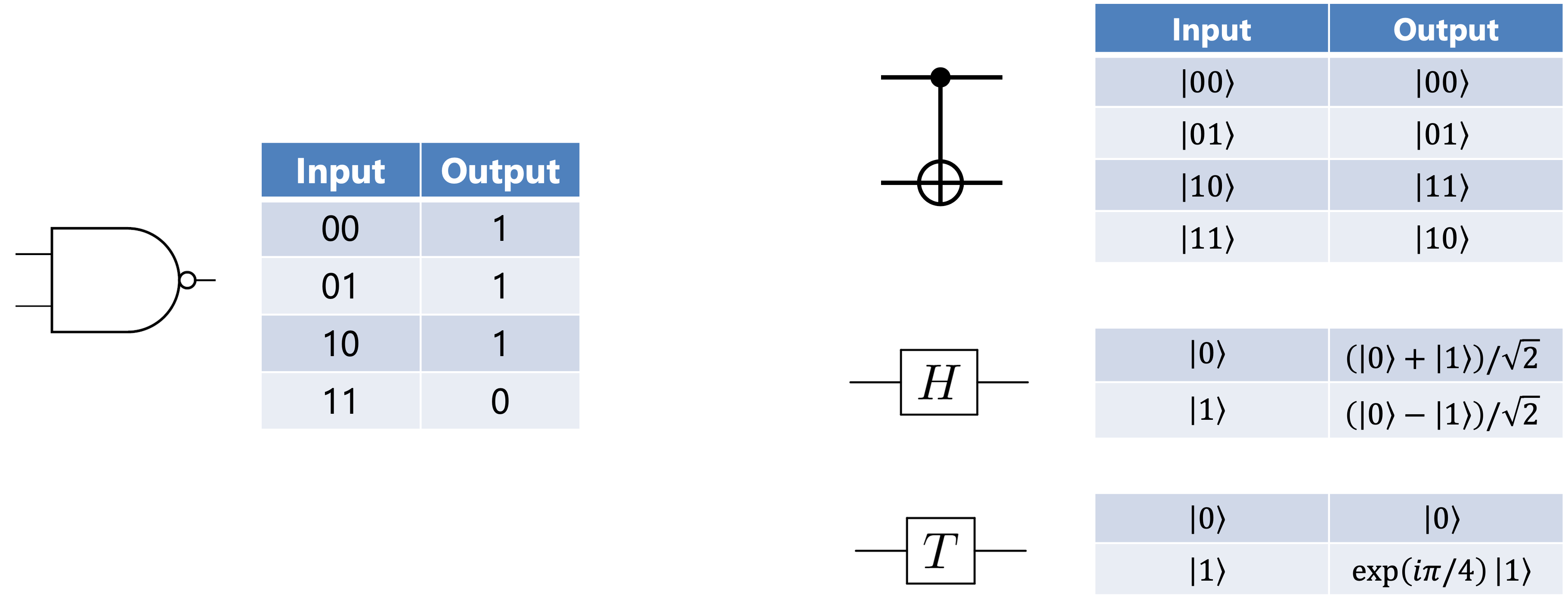
古典ゲートと量子ゲートの基本的な動作比較。 左側は古典論理ゲートの一例としてNANDゲートを示しており,その出力は「すべての入力が1でない限り1」となる非線形なブール関数です。右側は量子論理ゲートの代表例として,CNOTゲート(制御NOT),Hadamardゲート(重ね合わせを生成),およびTゲート(位相回転)をそれぞれ表しています。量子ゲートは線形かつ可逆であり,複数の状態を同時に操作できる特徴があります。特にHadamardゲートは重ね合わせ状態を生成し,Tゲートは位相を与えることで量子干渉に寄与します。これらのゲートは組み合わせることで,古典的には不可能な量子アルゴリズムを構築することが可能となります。
二重スリット実験と量子ビットの干渉のアナロジー
量子力学の有名な現象の一つに「二重スリット実験」があります。この実験では、電子や光などの粒子を1つずつスリットに向けて飛ばします。もしこれが普通の粒(たとえば小さな玉)のようなものであれば、2つのスリットのどちらかを通ってスクリーンに届くだけなので、スリットの形に対応した2つの山のような模様ができるはずです。
ところが実際には、粒子を1つずつ飛ばしても、スクリーン上には「しま模様(干渉縞)」が現れます。これは、粒子がスリットのどちらか一方を通るのではなく、2つのスリットを同時に通るように振る舞っているという、量子の不思議な性質を示しています。そして、スリットを通った後の経路に長さの違いがあると、それに応じた位相の差が粒子の波に生じ、波どうしが強め合ったり打ち消し合ったりして、干渉によるしま模様が現れるのです。
この現象は、高校の物理で学ぶ光の干渉と本質的に同じ仕組みです。たとえば、光を使ったヤングの二重スリット実験では、光波が2つのスリットを通る経路に応じて異なる位相を持ち、それらの波が干渉して明暗の縞模様ができます。量子力学では、光だけでなく電子や原子など、粒子的に見えるものまでもが波としての性質を持ち、同様の干渉を示すという点が特徴的です。
二重スリットの実験。 赤線が量子力学的な粒子の分布を示し、黒点線が古典的な粒子の分布を示しています。量子力学的な粒子は、2つのスリットを同時に通過するように振る舞い、その経路で獲得する「位相」の差 \(\Delta \theta\) が干渉を引き起こします。古典的な粒子は、2つのスリットのどちらか一方を通過するため、干渉は起こりません。
この現象は、量子ビットでも再現できます。まず、「0」の状態にある量子ビットに対して、\(R_y(\pi/2)\) というゲートをかけると、「0」と「1」の両方の状態が重ね合わさった状態になります。これは、ちょうど1つの粒子が2つのスリットを同時に通っていることに対応します。
次に、「0」の状態と「1」の状態にそれぞれ異なる「位相」を与える操作を行います。たとえば、「1」の状態にだけ角度θの位相を加えるには、 \(R_z(\phi)\) ゲートという操作を使います。これは、状態「0」に位相 \(-\phi/2\) 状態「1」に対してのみ複素位相 \(\phi/2\) を与える量子ゲートであり、ちょうど二重スリット実験において、2つのスリットからスクリーンまでの距離が異なるために生じる位相差に対応します。こうして、干渉が起こるための準備が整います。
最後に、 \(R_y(−\pi/2)\) というゲートをかけることで、最初に分けた2つの経路を再び合流させることができます。このとき、量子ビットを観測すると、「0」や「1」として出てくる確率が、途中で加えた位相 \(\theta\) によって変わります。これは、スクリーン上のどこに粒子が現れやすいかが、干渉によって変化することと同じです。
このように、量子ビットに対して適切な操作を行えば、二重スリット実験で見られるような「重ね合わせ」や「干渉」といった量子の性質を、量子コンピュータの中で再現することができます。
単一量子ビットのラムゼイ干渉回路。 太実線は量子ビットの振幅が辿る“経路”を示し,点線は初期状態 \(\vert 1\rangle\) に対応する空経路を表しています。最初の \(R_y(\pi/2)\) ゲートで \(\vert 0\rangle\) と \(\vert 1\rangle\) の重ね合わせを作り,中央の \(R_z(\phi)\) ゲートで二つの経路に位相差 \(\phi\) を付与,最後の \(R_y^{\dagger}\) ゲートで両経路を再結合します。経路間の位相差が干渉を引き起こし,測定確率は \(P(0)=\cos^{2}\tfrac{\phi}{2}\) と \(P(1)=\sin^{2}\tfrac{\phi}{2}\) に振動します。古典的にどちらか一方の経路しか通らない粒子であれば干渉は生じず,確率は常に \(\tfrac12\) に固定されます。
干渉を体験する実験:1量子ビットの量子回路を作ってみる
量子ビットの干渉を、実際に Python ライブラリ Cirq を使って体験してみましょう。古典コンピュータでも量子回路をシミュレートすることは可能で、量子ビットが 20 個程度までであれば、Google Colab のような環境でも問題なく実行できます。ここでは 1 量子ビットに対して「干渉縞」がどのように生じるかを観察する簡単な実験を行います。
Cirq とは?
Cirq は Google が開発している量子計算のための Python ライブラリで、量子ビットや量子ゲート、回路、シミュレーションなどを簡単に扱えます。
Google Colab とは
Google Colab は、Google が提供する Jupyter Notebook のクラウドサービスです。Google アカウントさえあれば、Python のコードをブラウザ上で実行できるため、特別な環境を用意しなくても手軽に量子計算の実験ができます。Colab では GPU や TPU を使った計算も可能で、量子コンピュータのシミュレーションにも適しています。使ったことがない人は、こちら を参考にしてみてください。
やってみよう:1量子ビットの干渉回路
以下の手順で干渉の様子を観察します。
- まず \(R_y(\pi/2)\) で量子ビットを「0」と「1」の重ね合わせ状態にします。
- 次に \(R_z(\theta)\) で各状態に位相差をつけます。
- 最後に \(R_y(-\pi/2)\) でそれぞれの状態を干渉させます。
- その状態を「観測」すると「0」になる確率が \(\theta\) によって振動します。
実行コード
Cirq のインストールには以下のコマンドを実行します。
# Cirq のインストール(初回のみ必要)
!pip install -q cirq
次に、以下のコードを実行してみましょう。
import cirq
import numpy as np
import matplotlib.pyplot as plt
# 量子ビットを1つ定義
q = cirq.NamedQubit("q0")
sim = cirq.Simulator()
# theta の値を 0 から 2π までスキャン
theta_vals = np.linspace(0, 2 * np.pi, 200)
prob_0 = []
for theta in theta_vals:
# 干渉回路の構築
circuit = cirq.Circuit(
cirq.ry(np.pi / 2)(q), # 初期重ね合わせ
cirq.rz(theta)(q), # 位相付与(干渉の原因)
cirq.ry(-np.pi / 2)(q), # 再合流
cirq.measure(q, key="m") # 測定
)
# シミュレーション(ショット数 = 1000)
result = sim.run(circuit, repetitions=1000)
counts = result.histogram(key="m")
prob_0.append(counts.get(0, 0) / 1000)
# 結果の可視化
plt.figure(figsize=(8, 4))
plt.plot(theta_vals, prob_0)
plt.xlabel(r"$\theta$")
plt.ylabel("P(0)")
plt.show()
量子ビットの測定結果は確率的であり、1回だけ測ってもその確率を知ることはできません。そこで、同じ量子回路を何度も実行(サンプリング)し、その結果の統計をとることで、ある出力が現れる確率を推定します。たとえば、ある量子状態に対して1000回測定を行い、そのうち「0」が800回、「1」が200回観測されたとすれば、「0」が出る確率はおおよそ0.8(80%)と見積もることができます。
Cirqでは、このような測定結果を sim.run(..., repetitions=1000) によって得ることができ、その結果は辞書のような形で result.histogram(key="m") に格納されます。これは、”m” という名前の測定結果に対して、各出力値(たとえば0や1)が何回出たかを記録したヒストグラム(度数分布表)です。
このヒストグラムから「0」が何回出たかを取り出すには、counts.get(0, 0) と書きます。ここで counts は result.histogram(...) で得られる辞書オブジェクトです。get(0, 0) は「キー0(つまり出力が0のとき)の値(回数)を取り出す。もしキーが存在しなければ0を返す」という意味です。これにより、「0」が出た回数を安全に取得し、それを1000で割ることで「0」になる確率を求めています。
結果と考察
上のコードを実行すると、以下のように \(\theta\) によって「0」が観測される確率 \(P(0)\) が滑らかな波(\(\cos^2(\theta/2)\))として変化することが分かります。これはまさに二重スリット実験で現れる干渉縞に相当し、量子ビットの状態の間に生じた「位相差」が観測確率に影響を与えている ことを示しています。 このような干渉は特にラムゼー干渉と呼ばれ、量子コンピュータの動作原理や量子ビットの性質を理解する上で重要な概念です。
干渉を応用する:Grover の探索アルゴリズム
ここまで見てきた「量子ビットの干渉」という現象は、量子アルゴリズムにおいて非常に重要な役割を果たします。その代表例が Grover のアルゴリズム です。
Grover のアルゴリズムとは?
Grover のアルゴリズムは、ある条件を満たすビット列(たとえば、何かのパスワードや特定の情報)を大量の候補の中から効率よく探し出すための量子アルゴリズムです。古典的なアルゴリズムでは、候補が \(N\) 個ある場合、最悪 \(O(N)\) 回の試行が必要になります。つまり、1個ずつ全部試していくしか方法がありません。
しかし Grover のアルゴリズムでは、量子ビットの重ね合わせと干渉をうまく利用することで、これを \(O(\sqrt{N})\) 回の操作で見つけ出すことができます。これは大規模な問題において非常に大きなスピードアップになります。
どのように動作するのか?
Grover のアルゴリズムは以下のような流れで進みます:
-
重ね合わせを作る:全てのビット列を一度に表現するような重ね合わせ状態(すべての状態が等しい振幅を持つ状態)を作ります。
-
目的のビット列にだけ位相を付ける:ある条件を満たすビット列に対してだけ符号(位相)を反転させる操作を行います。これにより、目的のビット列にだけマイナスの位相が付きます。
-
重ね合わせ状態に戻る方向への反射操作:全体の状態に対して「平均値に関して反転する」操作を行います。これにより、目的のビット列の振幅が強められ、それ以外が打ち消されるような干渉が起こります。
-
繰り返す:この一連の操作を \(O(\sqrt{N})\) 回繰り返すことで、目的のビット列が高い確率で測定される状態に到達します。
計算量の違い
- 古典的アルゴリズム:候補が \(N\) 個あるとき、平均して \(N/2\) 回、最悪 \(N\) 回の試行が必要。これは \(O(N)\) の計算量です。
- Grover のアルゴリズム:量子ビットの重ね合わせと干渉を活用して、\(O(\sqrt{N})\) 回の操作で目的のビット列を見つけることが可能です。
これは非常に大きな違いで、たとえば \(N=1,000,000\) の場合、古典では最大100万回必要な探索が、Grover では約1000回で済むことになります。
実行コード例(Cirq)
以下は、Grover のアルゴリズムを Cirq で実装した回路です。これは \(n\) 量子ビットを使って、「すべてのビットが 1」である状態(111…1)を探すような例です。
import cirq
def get_grover_circuit(n_iter, n_qubits):
qubits = [cirq.NamedQubit(s) for s in ['{}'.format(i) for i in range(n_qubits)]]
# Create a new circuit for Grover's algorithm
grover_circuit = cirq.Circuit()
# Apply Hadamard gates to all qubits to create superposition
grover_circuit.append(cirq.H.on_each(*qubits))
for i in range(n_iter):
oracle = cirq.Z.controlled(num_controls=n_qubits-1).on(*qubits) # flips 1111...
# Apply the oracle that flips the sign of 111..111 state
grover_circuit.append(oracle)
reflection = cirq.Circuit()
reflection.append(cirq.H.on_each(*qubits))
reflection.append(cirq.X.on_each(*qubits))
reflection.append(cirq.Z.controlled(num_controls=n_qubits-1).on(*qubits))
reflection.append(cirq.X.on_each(*qubits))
reflection.append(cirq.H.on_each(*qubits))
# Reflection about the |+++..+> state
grover_circuit.append(reflection)
return grover_circuit
# Print the Grover circuit
print("Grover Circuit:")
print(get_grover_circuit(1, 10))
このコードでは、n_iter=1、n_qubits=10 として 10 ビットの状態空間から 1 回の繰り返しで「1111111111」を探す回路を構成しています。繰り返し回数を増やすことで、より高い確率で目的のビット列を見つけることができます。
この回路が本当に正しく動いているか確認してみよう
さて、Grover のアルゴリズムでは、「正解のビット列」に対応する状態が、繰り返し操作を行うごとにどんどん強調されていきます。つまり、量子ビットが「正解の状態」に落ち着く確率がだんだん高くなっていくということです。これが本当にうまくいっているのか、実際に回路を動かして確認してみましょう。
以下のコードでは、量子ビットを 10 個使い、「すべてのビットが 1 の状態(1111111111)」を正解としたときに、Grover の操作を何回繰り返せばその状態が高い確率で現れるようになるかを調べます。
具体的には、繰り返し回数を 0 回から 24 回まで変えながら、それぞれの場合に「正解の状態」が出てくる確率をシミュレーションで計算しています。その結果をグラフにすることで、「ある回数で確率が最大になる」という Grover アルゴリズムの特徴が視覚的にわかるようになります。
n_max_iter = 25
n_qubits = 10
n_iter_list = np.arange(n_max_iter)
amplitude_list = []
for n_iter in n_iter_list:
grover_circuit = get_grover_circuit(n_iter, n_qubits)
simulator = cirq.Simulator()
result = simulator.simulate(grover_circuit)
# Check if the state is close to the solution state
amplitude_list.append(np.abs(result.final_state_vector[-1])**2)
import matplotlib.pyplot as plt
plt.plot(n_iter_list, amplitude_list)
plt.xlabel('Number of iterations')
plt.ylabel('Probability of the solution')
plt.show()
以下のようなグラフが表示されるはずです。グラフでは、横軸が「繰り返し回数(何回 Grover 操作を行ったか)」、縦軸が「正解の状態(111…1)が出る確率」を表しています。
「1111…1 を探す」のはあくまで例です
さきほどのコードでは「すべてのビットが 1 の状態(111…1)を探す」という例で Grover のアルゴリズムを紹介しましたが、これはあくまで量子回路のわかりやすさを優先して、例として出したものです。本当の Grover のアルゴリズムでは、「どのビット列が正解か」を決める ルール(関数) を使って、その正解だけに「マイナスの位相(符号の反転)」をつける操作が必要です。このルールは、たとえば「この条件を満たすビット列だけが正解」といった 判断基準 です。この判断基準を使って、「そのビット列が正解なら−1倍、そうでなければ何もしない」というような操作をつくる必要があります。コードの中ではこれを oracle と呼んでいますが、本来はこの部分を、自分が探したいものに合わせて関数として設計する必要があります。
たとえば、「ある条件に合うパスワードを探したい」とか、「特定の特徴をもつデータだけを見つけたい」といった場面では、それに応じた oracle(オラクル)を自分で作ることになります。だから Grover のアルゴリズムを実際に使うときは、「正解をどうやって見分けるのか?」をうまく組み込み、それを量子回路として落とし込む工夫が大事になるんです。
実はちょっとした注意点もあります
Grover のアルゴリズムはたしかにすごいのですが、万能な方法というわけではありません。特に注意してほしいのは、「何を探すのか」を決める条件(関数のようなもの)がどんなふうに与えられているかによって、量子コンピュータの強みが変わってくるという点です。
このアルゴリズムのすごさは、中身のわからない“ブラックボックス”な条件に対して「何回質問すれば目的の答えにたどり着けるか」という意味で優れているということです。つまり、「このビット列が正解かどうかを教えてくれる箱」に対して、なるべく少ない回数で質問できるのが強みです。でも、もしその関数の中身(条件のルール)が はじめから数式などでハッキリわかっている 場合には、古典的な方法で工夫してすばやく解くことができるかもしれません。そういうときには、Grover のアルゴリズムの出番があまりないこともあります。
言い換えれば、「何が正解かをチェックする方法が“箱の中に隠されている”ようなとき」にこそ、このアルゴリズムの強みが最大限に発揮される、ということです。使いどころを間違えないことも、量子アルゴリズムを学ぶうえで大切な視点です。
まとめ:量子の世界をちょっとだけ体験してみよう
この記事では、「量子ビットって何?」「どうして干渉が起こるの?」「それが計算にどう役立つの?」という基本的な問いに答えながら、実際に Python と Cirq を使って量子回路を動かしてみる体験をしてきました。
特に、重ね合わせと干渉という量子の特徴が、Grover のような強力なアルゴリズムにつながっていることを見てもらいました。こうした量子の性質は、直感的には不思議で難しそうに感じるかもしれませんが、少しずつ手を動かして確かめることで、身近なものとして理解できるようになります。
そして何より、量子コンピュータはもう未来の話ではなく、すでに動いている現実の技術です。みなさんが今日使った Cirq や Google Colab を使えば、量子アルゴリズムの基本を自分の手で実験しながら学ぶことができます。興味を持った人は、ぜひこの先も自分で回路をいじってみたり、新しいアルゴリズムに挑戦してみたりしてください。
もっと学びたい人へ:私たちの研究グループを紹介します
この企画は、大阪大学 大学院基礎工学研究科電子光領域に所属する御手洗グループが執筆しました。御手洗は、大阪大学の 量子情報・量子生命研究センター(QIQB) にも所属しており、QIQB 内の他の研究グループと緊密に連携しながら、量子情報科学の最先端研究を進めています。
私たちの研究グループでは、
- 量子機械学習や量子化学シミュレーションなどの量子アルゴリズムの研究
- 実際の量子ハードウェアを使った実機実験
- 現実世界の問題に量子計算をどう応用するかという応用的な研究
などを行っており、「理論から実機応用まで」をカバーする幅広いテーマに取り組んでいます。もしこの記事を読んで「もっと知りたい!」と思ったら、ぜひ以下のリンクから研究室や QIQB の情報をチェックしてみてください。
- 御手洗グループのウェブサイト: https://mitarai.qc.ee.es.osaka-u.ac.jp
- QIQB(量子情報・量子生命研究センター): https://qiqb.osaka-u.ac.jp
- IPSJ-ONE 2025 での講演動画
量子の世界はまだまだ未知のことだらけ。でも、だからこそ一緒に新しい発見をしていく仲間を、私たちはいつでも歓迎しています!
それでは、ここまで読んでいただきありがとうございました!
いちょう祭が、みなさんにとって量子の世界と出会う小さなきっかけになればうれしいです。



